目次
はじめに
皆さん、物理学は好きですか??
物理学なんか国試の勉強以来してないよって方もいらっしゃるのではないでしょうか??(もし勉強していた方がいたらすいません^^;)
しかし、臨床にでたら意外と物理学的知識って使いませんか??
僕は患者に説明するときなんかに使う時が多いです!
いちばん使うのが猫背の方ですね。
例えば・・・
『猫背になることにより、土台となって頭を支えている胸から頭が前方に位置していますよね。
実は物体というのは支えるところから離れれば離れるほど重くなるんです。
つまり頭が前に行けばその分だけ首周囲の筋に負担がかかってきます。
また、首の筋肉はそこまで大きい筋肉ではないので、すぐ疲れやすい状態に陥ってしまいます。
首の筋肉が疲れてくると肩こりや、頭痛の原因にもなってくるんです。
つまり猫背という姿勢はよくないんですよ。』
っていう感じに説明しています。
特に男性の方は左脳タイプの方が多く、論理的に物事を考える方が多いそうです。
そういった方に、物理学的知識を織り交ぜながら順序良く話していくと、納得してもらえますよね!
そうなると、信頼関係ができ少なくとも後の治療展開が楽になってきます。
そうなるためにも、物理学の知識を自分で噛み砕いて説明できるようになることが必要なことではないでしょうか。
ということで、今回はなるべくわかりやすく物理学について書いていきたいと思いますのでよろしくお願いします!
物理学用語の解説
内力と外力
筋や骨を動かしたり、安定させる力は2つに分かれます。
それが内力と外力です。
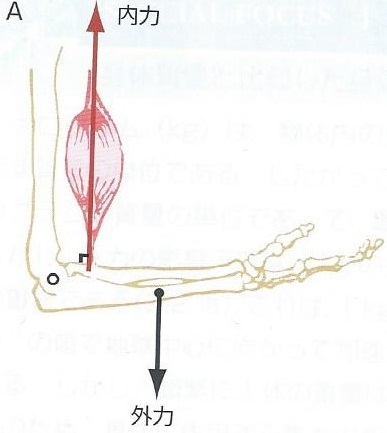
(筋骨格系のキネシオロジーから引用
内力とは、体の内部でおこる力のことをいい、内力は『自動的』と『他動的』に分かれてきます。
自動的な力とは筋によって生じる力のことを指します。
他動的な力とは結合組織、靭帯、関節包を含む伸長された関節周囲内の緊張によって生じる力のことをいいます。
外力とは、外部由来の力よって生じる力のことをいいます。
具体例としては、重力・荷物・重錘・セラピストが与える抵抗などのことです。
力
力とは、物体を押したり引いたりして線的に動かすものです。
モーメントアーム
モーメントアームとは、支点から力の作用点までの距離のことをいいます。
このモーメントアームが長くなれば長くなるほど、より多くの力を生じさせます。
トルク(モーメント)
モーメントアームと力の積をトルク(モーメント)といいます。
力とトルクの違いとして、力は線的な動きのことを指し、トルクは回転させる力のことを指します。
先ほどモーメントアームが長いほど多くの力が生じるということを説明しました。
例として野球で考えてみます。

ホームランバッターや、ホームランを狙う時は基本的にバットを長く持ってますよね??
これは支点から作用点までのモーメントアームを長くして、より多くのトルクを生み出しボールを遠くにとばしたいからということがわかります。
外的トルク・内的トルク
内的トルクとは、内力(筋)と内的モーメントアームの積で表せるトルクのことです。
外的トルクとは、外力(例えば重力)と外的モーメントアームの積で表せるトルクのことです。
また図を見ながら考えていきます。
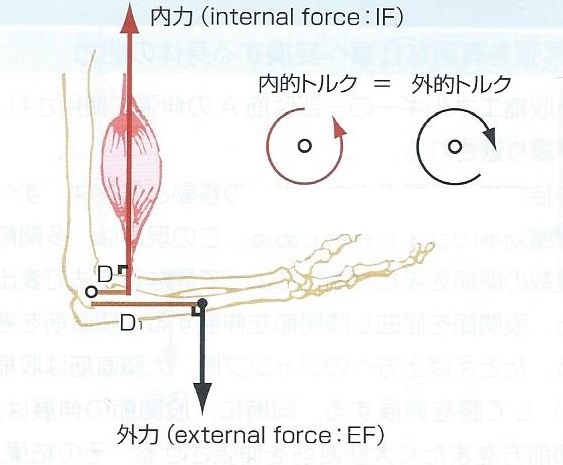
(筋骨格系のキネシオロジーから引用
この肘の図で考えると、赤線が内的トルク(上腕二頭筋による筋収縮)、黒線が外的トルク(重力)になります。
この図の肘は、内的トルク、外的トルクが等しい状態なので、つりあっていて静止しています。
まあイラストなので当たり前ですが(笑)
これを静的回転平衡というらしいです。これは別に覚えなくてもいいかもしれません(笑)
臨床では必須!!ニュートンの運動法則を生体力学に当てはめてみよう
何故必須なのか??
臨床で姿勢を評価をするとき、
「あそこの関節のあの筋肉に負荷がかかってそうだな」
とか考えますよね??
その後に、
「となると、ここの筋肉の緊張を落として、あっちの筋肉を賦活させて体のバランスを整えよう」
などという治療プログラムを立案しますよね??
この時にニュートンの運動法則を理解していると、より柔軟かつ多様で豊かな評価や、治療アイデアが浮かんでくると思います。
なので非常に重要なポイントとなってくるので是非この機会に理解を深めましょう!
ニュートンの第1法則:慣性の法則
第1法則は慣性の法則ともいいます。
[aside type="normal"]慣性とは
物体に力が働いていない時、速度を保ち続ける性質を慣性という。
例として、電車に乗っているとします。
発車する時は進行方向とは反対に慣性が働き、減速する時は、進行方向に慣性が働きます。[/aside]
ニュートンの第1法則では質量が重くなったり、質量中心から離れば離れるほど慣性モーメントが増えていくということを説明しています。 [aside type="normal"]慣性モーメントとは回転のしにくさと捉えてもらえれば大丈夫です。[/aside]
分かりやすい例でいくと、水泳の飛び込み選手がいますよね?? 空中で連続宙返りを成功させる為には、腕で下肢を抱え込みますよね?? また頭を膝に近づけ、身体質量を回転軸により近づけようとしていることがわかります。 (筋骨格系のキネシオロジーから引用 力(F).質量(m)、加速度(a)の関係性を示します。 基本的にF=maという式で表されています。 例えば力が0の場合、加速度も0になります。 また物体に力が加わり、加速度が生じた時物体は力の方向へ動きます。 また角加速度の大きさはトルクに比例していきます。しかし慣性モーメントは大きくなります。 つまりトルクが大きくなればなるほど、スピードがおそくなります。 反対にトルクが小さくなればなるほど、スピードは速くなっていきます。 ニュートンの第3法則では、すべての作用に対して、等しい大きさで反対方向の反作用があるといわれています。 おそらくニュートンの作用‐反作用の法則のもっとも適切な臨床での応用は、人が歩行時に床から受ける反作用ではないでしょうか?? 足部は踵接地の際に、床に力を及ぼします。 その時に、床からの方向が反対で大きさの等しい力、つまり床反力が働きます。 床反力は歩行中、大きさ、方向、床反力の作用点の位置は変化します。 つまり釣り合っている状態にあるといえます。 今回は物理学について書いてみました。 普段なんとなく説明していませんか?? 今回の記事を読み、もう一度教科書や参考書を開いて見直してみるきっかけになればいいと思います。 またここは違うんじゃないか、補足事項などがあればまた教えていただけると助かります(^_^;) 最後までご覧いただきありがとうございました。 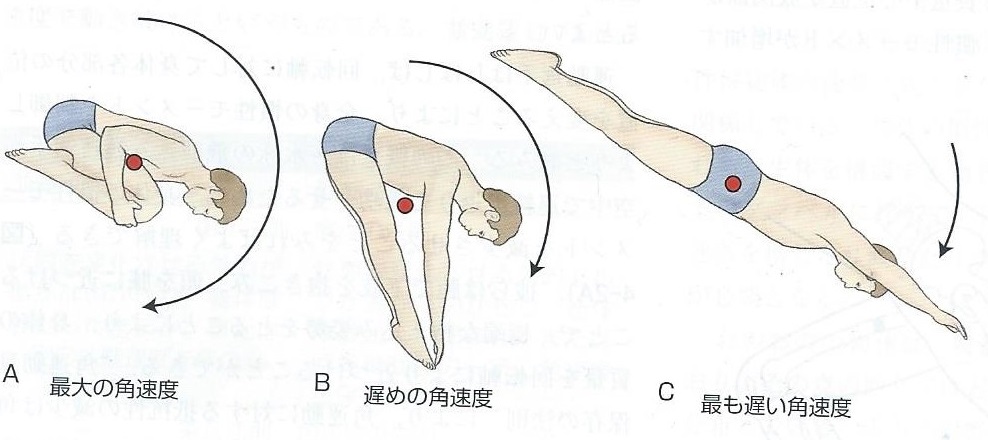
ニュートンの第2法則:加速度の法則
ニュートンの第3法則:作用-反作用の法則

終わりに









